Answer:
The probability that a pipe produced has length greater than 30 feet is 0.5385.
Explanation:
Let X = product lengths of the pipes produced by a company.
The random variable X is Uniformly distributed with parameters a = 28.50 feet to b = 31.75 feet.
The probability density function of Uniform random variable is:
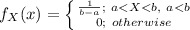
Compute the probability that a pipe produced has length greater than 30 feet as follows:
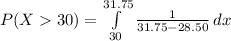
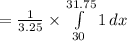
![=(1)/(3.25)* [31.75-30]](https://img.qammunity.org/2021/formulas/mathematics/college/zc757gjvf1j1ewydzmyl12old33s0nyeyr.png)
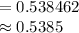
Thus, the probability that a pipe produced has length greater than 30 feet is 0.5385.