Answer:
Discriminant: -4
No real solutions
Explanation:
You might remember this long, seemingly very hairy thing called the quadratic formula from earlier in algebra:

The discriminant of a quadratic equation of the form
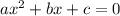 is that bit under the square root:
is that bit under the square root:
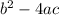 . What does the discriminant tell us? Since we're taking its square root, we know that
. What does the discriminant tell us? Since we're taking its square root, we know that
 is only real for non-negative values of
is only real for non-negative values of
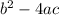 . If
. If
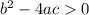 , we have two real roots, one for
, we have two real roots, one for
 and one for
and one for
 . If
. If
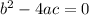 , the function has a rational root, since the formula becomes
, the function has a rational root, since the formula becomes
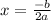
In your case, we have the equation
 ; here,
; here,
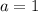 ,
,
 , and
, and
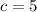 , so our discriminant is
, so our discriminant is
 . Since we'd have a negative under our square root in the quadratic formula, we have no real solutions.
. Since we'd have a negative under our square root in the quadratic formula, we have no real solutions.