Question

please help!!!!!!!!! Rena used the steps below to evaluate the expression (StartFraction (x Superscript negative 3 Baseline) (y Superscript negative 2 Baseline) Over 2 (x Superscript 4 Baseline) (y superscript negative 4 Baseline) EndFraction) Superscript negative 3, when x = negative 1 and y = 2. Step 1: Substitute x = negative 1 and y = 2 into the expression. (StartFraction (negative 1) Superscript negative 3 Baseline (2) Superscript negative 2 Baseline Over 2 (negative 1) Superscript 4 Baseline (2) superscript negative 4 Baseline) EndFraction) Superscript negative 3 Step 2: Simplify the parentheses. (StartFraction (2) Superscript 4 Baseline Over 2 (negative 1) Superscript 4 Baseline (negative 1) cubed (2) squared EndFraction) Superscript negative 3 Baseline = (StartFraction (2) squared Over 2 (negative 1) Superscript 7 Baseline EndFraction) Superscript negative 3 Step 3: Evaluate the power to a power. StartFraction (2) Superscript negative 6 Baseline Over 2 Superscript negative 3 Baseline (negative 1) Superscript negative 21 baseline EndFraction Step 4: Use reciprocals and find the value. StartFraction 1 Over 2 cubed (2) Superscript 6 Baseline (negative 1) Superscript 21 Baseline EndFraction = StartFraction 1 Over 8 times 64 times (negative 1) EndFraction = Negative StartFraction 1 Over 512 EndFraction In which step did Rena make the first error? Step 1 Step 2 Step 3 Step 4

Answer 1

Step 4/D is correct

Explanation:

Answer 2

9514 1404 393

Answer:

Step 4

Explanation:

Step 4 should look like ...

`(2^3\cdot(-1)^(21))/(2^6)=(-8)/(64)=-(1)/(8)`

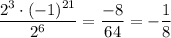
All steps up to that point are correct. Step 4 has the first error.

_____

Comment on the question

It took about 15 minutes to translate the mishmash provided in this problem statement into something sensible. A picture or math symbols are much preferred. At the very least, some line spacing or formatting of the text would be useful.