Question

Of the members of the Spring Lake Bowling Lanes, 57% have a lifetime membership

and bowl regularly (three or more times a week). If 70% of the club members bowl
regularly, find the probability that a randomly selected member is a lifetime member,
given that he or she bowls regularly.
a) 0.056
b) 0.814
c) 0.533
d) 0.538

Answer 1

The probability that a randomly selected member is a lifetime member, given that he or she bowls regularly is 0.814, option b

Explanation:

Let "M" denotes the event that a club member has a lifetime membership and "B" be denotes the event that the club member bowls.

57% of the members have lifetime membership and bowl regularly. This means, the probability that a randomly selected member has a lifetime membership and bowls regularly =
`P(M \cap B)=57\%=0.57`

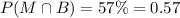
70% of the club members bowl. This means, the probability that a randomly chosen member bowls = P(B) = 70% = 0.70

We have to find the probability that a randomly selected member is a lifetime member, given that he or she bowls regularly. This is conditional probability which can be expressed mathematically as P(M | B)

The formula to calculate the conditional probability is:

`P(A|B)=(P(A \cap B))/(P(B))`

So, the formula for our case will be:

`P(M|B)=(P(M \cap B))/(P(B))`

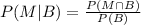
Using the values in this formula we get:

`P(M|B)=(0.57)/(0.70)=0.814`

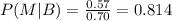
This means, the probability that a randomly selected member is a lifetime member, given that he or she bowls regularly is 0.814