Looks like
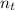 is the number of subintervals you have to use with the trapezoidal rule, and
is the number of subintervals you have to use with the trapezoidal rule, and
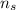 for Simpson's rule. In the attachments, I take both numbers to be 4 to make drawing simpler.
for Simpson's rule. In the attachments, I take both numbers to be 4 to make drawing simpler.
Split up the integration interval [1, 8] into n subintervals. Each subinterval then has length (8 - 1)/n = 7/n. This gives us the partition
[1, 1 + 7/n], [1 + 7/n, 1 + 14/n], [1 + 14/n, 1 + 21/n], ..., [1 + 7(n - 1)/n), 8]
The left endpoint of the
 th interval is given by the arithmetic sequence,
th interval is given by the arithmetic sequence,
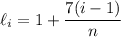
and the right endpoint is
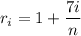
both with
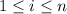 .
.
For Simpson's rule, we'll also need to find the midpoints of each subinterval; these are
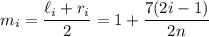
The area under the curve is approximated by the area of 12 trapezoids. The partition is (roughly)
[1, 1.58], [1.58, 2.17], [2.17, 2.75], [2.75, 3.33], ..., [7.42, 8]
The area
 of the
of the
 th trapezoid is equal to
th trapezoid is equal to
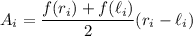
Then the area under the curve is approximately
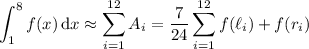
You first need to use the graph to estimate each value of
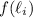 and
and
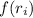 .
.
For example,
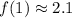 and
and
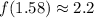 . So the first subinterval contributes an area of
. So the first subinterval contributes an area of
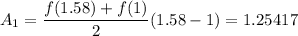
For all 12 subintervals, you should get an approximate total area of about 15.9542.
Over each subinterval, we interpolate
 by a quadratic polynomial that passes through the corresponding endpoints
by a quadratic polynomial that passes through the corresponding endpoints
 and
and
 as well as the midpoint
as well as the midpoint
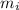 . With
. With
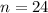 , we use the (rough) partition
, we use the (rough) partition
[1, 1.29], [1.29, 1.58], [1.58, 1.88], [1.88, 2.17], ..., [7.71, 8]
On the
 th subinterval, we approximate
th subinterval, we approximate
 by
by
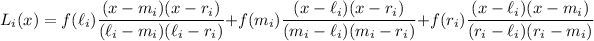
(This is known as the Lagrange interpolation formula.)
Then the area over the
 th subinterval is approximately
th subinterval is approximately
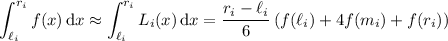
As an example, on the first subinterval we have
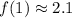 and
and
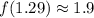 . The midpoint is roughly
. The midpoint is roughly
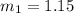 , and
, and
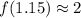 . Then
. Then
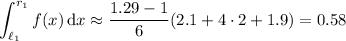
Do the same thing for each subinterval, then get the total. I don't have the inclination to figure out the 60+ sampling points' values, so I'll leave that to you. (24 subintervals is a bit excessive)
For part 2, the average rate of change of
 between the points D and F is roughly
between the points D and F is roughly
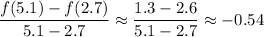
where 5.1 and 2.7 are the x-coordinates of the points F and D, respectively. I'm not entirely sure what the rest of the question is asking for, however...