Question

Simplify the expression: sin (2x) cos (5x) − sin (5x) cos (2x).

a. cos(-3x)
b. cos(7x)
c. sin(-3x)
d. sin(7x)

Answer 1

Given:

The given expression is
`sin (2x) \ cos (5x) - sin (5x) \ cos (2x)`

We need to determine the simplified value of the given expression.

Simplification:

Since, the given expression is in the form of
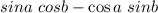`sin a \ cos b-\cos a \ sin b`, the given expression can be simplified using the identity
`\sin (a-b)=\sin a \cos b-\cos a \sin b`

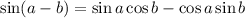
Comparing the given expression with the identity, we get;

`a=2x` and
`b=5x`

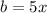
Using this in the identity, we get;

`sin (2x) \ cos (5x) - sin (5x) \ cos (2x)=sin(2x-5x)`

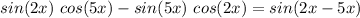
Simplifying, we get;

`sin (2x) \ cos (5x) - sin (5x) \ cos (2x)=sin(-3x)`

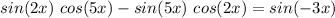
Thus, the simplified value of the given expression is
`sin (-3x)`

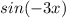
Hence, Option c is the correct answer.