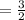Question

Enter the values for the highlighted variables to complete the steps to the sum (3x)/(2x - 6) + 9/(6 - 2x) = (3x)/(2x - 6) + 9/(a(2x - 6)) = 3x 2x-6 + 6 2x-6 = 3x-c 2x-6 = d(x-x) f(x-3) =g

Answer 1

Answer:a= -1

b= -9

c=9

d=3

e=3

f=2

g=1.5

Explanation:

Answer 2

a= -1

b= -9

c=9

d=3

e=3

f=2

`g=\frac32`

Explanation:

Rule of sign:

1. (-)×(+)=(-), (-)÷(+)=(-)
2. (+)×(-)=(-) , (+)÷(-)=(-)
3. (+)×(+)=(+), (+)÷(+)=+
4. (-)×(-)=(+), (-)÷(-)=(+)

Given that,

`(3x)/(2x-6)+(9)/(6-2x)`

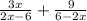
We can rewrite 6-2x as 2x-6, taking (-1) as common factor of (6-2x)

`=(3x)/((2x-6))+(9)/(-1(2x-6))`

So, a= -1

`\frac9{-1}=-9`

`=(3x)/((2x-6))+(-9)/((2x-6))`

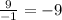
So, b= -9

The L.C.M of (2x-6) and (2x-6) is (2x-6)

and (2x-6)÷(2x-6)=1

`=(1 * 3x+1* (-9))/((2x-6))`

`=(( 3x-9))/((2x-6))`

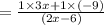
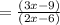
∴c= 9

(3x-9) has a common factor 3 and (2x-6) has a common factor 2.

(3x-9)=3(x-3)

(2x-6)=2(x-3)

`=(3(x-3))/(2(x-3))`

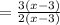
∴d=3, e=3 and f=2

Since the denominator and numerator are the product of two polynomial. So, if there is any common element, then can cancel the common factor.

Here the common factor is (x-3). So cancel out (x-3).

`=\frac32`

`\therefore g=\frac32`