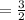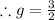Answer:
a= -1
b= -9
c=9
d=3
e=3
f=2
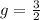
Explanation:
Rule of sign:
- (-)×(+)=(-), (-)÷(+)=(-)
- (+)×(-)=(-) , (+)÷(-)=(-)
- (+)×(+)=(+), (+)÷(+)=+
- (-)×(-)=(+), (-)÷(-)=(+)
Given that,
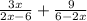
We can rewrite 6-2x as 2x-6, taking (-1) as common factor of (6-2x)
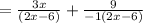
So, a= -1
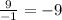
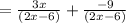
So, b= -9
The L.C.M of (2x-6) and (2x-6) is (2x-6)
and (2x-6)÷(2x-6)=1
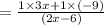
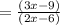
∴c= 9
(3x-9) has a common factor 3 and (2x-6) has a common factor 2.
(3x-9)=3(x-3)
(2x-6)=2(x-3)
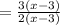
∴d=3, e=3 and f=2
Since the denominator and numerator are the product of two polynomial. So, if there is any common element, then can cancel the common factor.
Here the common factor is (x-3). So cancel out (x-3).