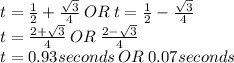Question

A projectile is launched from a hole in the ground one foot deep. Its height follows the equation h=-16t^2+8t-1 . Use factoring by perfect-squares to find the time when the projectile lands back on the ground.

Answer 1

t=0.93 seconds or t=0.07 seconds

Explanation:

If
`h=-16t^2+8t-1`

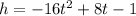
The time when the projectile lands on the ground is when its height, h=0.

`-16t^2+8t-1=0`

Using Factoring by Perfect Squares

`-16t^2+8t=1\\\text{Divide all through by the coefficient of t^2}\\(-16t^2)/(-16) +(8t)/(-16)=(1)/(-16)\\t^2-(1)/(2)t=-(1)/(16)`

Divide all through by the coefficient of
`t^2`

`(-16t^2)/(-16) +(8t)/(-16)=(1)/(-16)\\t^2-(1)/(2)t=-(1)/(16)`

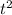
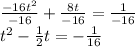
Next, divide the coefficient of t by 2, square it and add it to both sides.

`t^2-(1)/(2)t+(-(1)/(2))^2=-(1)/(16)+(-(1)/(2))^2\\(t-(1)/(2))^2=-(1)/(16)+(1)/(4)\\(t-(1)/(2))^2=(3)/(16)\\`

Taking square roots of both sides

`t-(1)/(2)=\sqrt{(3)/(16)}\\t=(1)/(2) \pm \sqrt{(3)/(16)}\\t=(1)/(2) \pm (√(3))/(4)`

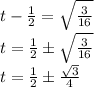
Therefore:

`t=(1)/(2) + (√(3))/(4) \: OR \: t=(1)/(2) - (√(3))/(4)\\t=(2+√(3))/(4) \: OR \: (2-√(3))/(4)\\t=0.93seconds \: OR \: 0.07 seconds`