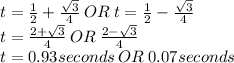Answer:
t=0.93 seconds or t=0.07 seconds
Explanation:
If
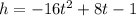
The time when the projectile lands on the ground is when its height, h=0.
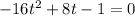
Using Factoring by Perfect Squares

Divide all through by the coefficient of
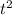
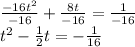
Next, divide the coefficient of t by 2, square it and add it to both sides.
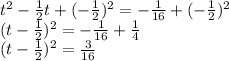
Taking square roots of both sides
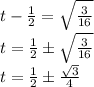
Therefore: