Question

Bobby knows that the perimeter of the original rectangle is 120 meters. He also knows that the perimeter of the reduced rectangle is 30 meters and the reduced length is 9 meters. A small rectangle has a length of 9 meters. A larger rectangle is blank. Not drawn to scale What is the width of the original rectangle? 20 meters 24 meters 36 meters 48 meters

Answer 1

b 24 meters

Explanation:

ed

Answer 2

24 meters is the width of the original rectangle.

Explanation:

Given:

Bobby knows that the perimeter of the original rectangle is 120 meters. He also knows that the perimeter of the reduced rectangle is 30 meters and the reduced rectangle has a length of 9 meters.

Now, to get the width of original rectangle.

The reduced rectangle's perimeter = 30 meters.

The reduced rectangle's length = 9 meters.

Now, we find the width of reduced rectangle by using formula:

Let the width of reduced rectangle be
`x.`

`Perimeter=2* length+2* width`

`30=2* 9+2* x`

`30=18+2x`

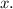
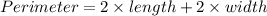
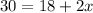
Subtracting both sides by 18 we get:

`12=2x`

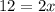
Dividing both sides by 2 we get:

`6=x\\\\x=6\ meters.`

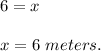
The width of reduced rectangle = 6 meters.

Now, to get the width of original rectangle:

Let the width of original rectangle be
`w.`

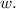
As given, the perimeter of the original rectangle = 120 meters.

And, the perimeter of reduced rectangle is 30 meters and its width is 6 meters.

So, 30 is equivalent to 6.

Thus, 120 is equivalent to
`w.`

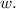
Now, to get the width using cross multiplication method:

`(30)/(6)=(120)/(w)`

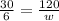
By cross multiplying we get:

`30w=720`

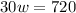
Dividing both sides by 30 we get:

`w=24\ meters.`

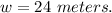
The width of original rectangle = 24 meters.

Therefore, 24 meters is the width of the original rectangle.