Answer:
the first statement is true
Explanation:
The side- splitter states that if the line is parallel to a side of the triangle and it intersects the other 2 sides, it divides those sides proportionally.
Thus the converse is that if the sides are proportional then the side TU is parallel to the side RS
Calculating the ratios
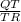 =
=
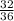 =
=
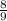
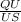 =
=
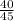 =
=
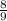
Since the ratios are equal then TU is parallel to RS