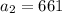Question

a cell phone company plans to market a new smartphone. they have already sold 612 units durning the first week of the campaign. they plan to increase sales by 8% each week. for example, they plan to sell about 661 units durning week 2. they want to continue this for a year (52 weeks)

Answer 1

The first term is 612.

The common ratio is 1.08 and

The recursive rule is
`a_(n) = a^(n-1) * r`

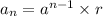
Explanation:

the question to the problem is to write the values of the first term, common ratio, and expression for the recursive rule.

The first term :

In geometric sequence, the first term is given as
`a_(1)`.

⇒
`a_(1) = 612`

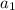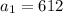
Now, the geometric sequence follows as 612, 661, ........

The common ratio (r) :

It is the ratio between two consecutive numbers in the sequence.

Therefore, to determine the common ratio, you just divide the number from the number preceding it in the sequence.

⇒ r = 661 divided by 612

⇒ r = 1.08

To find the recursive rule :

A geometric series is of the form a,ar,ar2,ar3,ar4,ar5........

Here, first term
`a_(1) = a` and other terms are obtained by multiplying by r.

• Observe that each term is r times the previous term.
• Hence to get nth term we multiply (n−1)th term by r .

The recursive rule is of the form
`a_(n) = a^(n-1) * r`

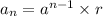
This is called recursive formula for geometric sequence.

We know that r = 1.08 and
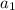`a_(1)` = 612.

To find the second term
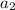`a_(2)`, use the recursive rule
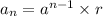
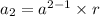
`a_(n) = a^(n-1) * r`

⇒
`a_(2) = a^(2-1)* r`

⇒
`a_(2) = a^(1)* r`

⇒
`a_(2) = 612* 1.08`

⇒
`a_(2) = 661`