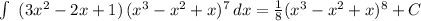Question

Find the indefinite integral. (Use C for the constant of integration.)

(3x^2 − 2x + 1)(x^3 − x^2 + x)^7 dx

Answer 1

`\int\ {(3x^2-2x+1)\,(x^3-x^2+x)^7} \, dx = (1)/(8) (x^3-x^2+x)^8+C`

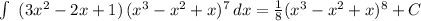
tep-by-step explanation:

In order to find the integral:

`\int\ {(3x^2-2x+1)\,(x^3-x^2+x)^7} \, dx`

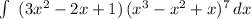
we can do the following substitution:

Let's call

`u=(x^3-x^2+x)`

Then

`du = (3x^2-2x+1) dx`

which allows us to do convert the original integral into a much simpler one of easy solution:

`\int\ {(3x^2-2x+1)\,(x^3-x^2+x)^7} \, dx = \int\ {u^7 \, du = (1)/(8) \,u^8 +C`

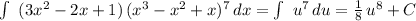
Therefore, our integral written in terms of "x" would be:

`\int\ {(3x^2-2x+1)\,(x^3-x^2+x)^7} \, dx = (1)/(8) (x^3-x^2+x)^8+C`