Question

You will need your ticker code (company abbreviation) for stock prices for this question. Use your ticker code to obtain the closing prices for the following two time periods to obtain two data sets: March 2, 2019 to March 16, 2019 Data set A February 16, 2019 to February 28, 2019 Data set B Take the closing prices from data set B and add 0.5 to each one of them. Treat data sets A and B as hypothetical sample level data on the weights of newborns whose parents smoke cigarettes (data set A), and those whose parents do not (data set B). a) Conduct a hypothesis test to compare the variances between the two data sets. b) Conduct a hypothesis to compare the means between the two data sets. Selecting the assumption of equal variance or unequal variance for the calculations should be based on the results of the previous test. c) Calculate a 95% confidence interval for the difference between means. • Data set A: total= 677.98, mean= 67.798, n= 10, variance= 0.663084, std devition= 0.814299972 • Data set B: total= 574.24, mean=71.78, n=8, variance= 0.727143, std devition= 0.8527267191. Do not use excel function for p value. 2. Show all your work

Answer 1

a) Calculated value F = 1.088 < 3.29

null hypothesis is accepted

Therefore there is no difference between the variances.

b) t = 8.79 > 1.746 for 16 degrees of freedom at 95% level of significance.

The null hypothesis is rejected.

we do not compare means between the two data sets

c) The 95 % of confidence intervals for the difference between means

are (3.30 ,4.68)

Explanation:

Given data

Data set A Data set B

Total 677.98 Total 574.24,

n₁= 10 n₂=8

mean((x₁⁻) = 67.798 mean( x₂⁻) = 71.78

variance(S₁²) = 0.663084 variance(S₂²)= 0.727143

S.D(S₁) = 0.814299972 S.D(S₂) = 0.8527267191

a) Null hypothesis (H₀) : σ₁² = σ₂²

Alternative hypothesis: σ₁² ≠ σ₂²

The compare of variances we will use the test statistic is F - distribution

`F = (S^(2) _(2) )/(S^(2) _(1) ) ( S^(2) _(2)>S^(2) _(1))`

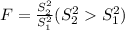
given data total= 677.98

∑(x-x⁻ )² = 677.98

Given data ∑(y-y⁻ )² = 574.24

S₁² =
`(∑(x-x⁻ )²)/(n_(1) -1) = (677.98)/(10-1) =75.33`

`S2² = (∑(y-y⁻ )²)/(n_(2) -1) = (574.24)/(8-1) =82.03`

`F = (82.03)/(75.33) =1.0889`

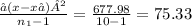
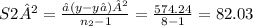
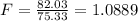
The degrees of freedom ν = ( n₁-1, n₂-1) = (10-1 ,8-1) = (9 , 7)

Tabulated value of F for (9 , 7) degrees of freedom at 5% level of significance is 3.29 (see 'F' table at 0.05 level )

Conclusion:-

Calculated value F = 1.088 < 3.677

null hypothesis is accepted

Therefore there is no difference between the variances.

b)

Null hypothesis (H₀) : μ₁ - μ₂≤ D ( given data D= 0.5 add to each data

Alternative hypothesis: μ₁ - μ₂≥ D

Sample statistic :- (x₁⁻ - x₂⁻)

Estimated standard error:-

standard error (S. e) =
`\sqrt{(S_(1) ^(2) )/(n_(1) ) +(S_(2) ^(2) )/(n_(2) ) }`

Test statistic 't'

`t = \frac_-D {\sqrt{(S_(1) ^(2) )/(n_(1) ) +(S_(2) ^(2) )/(n_(2) ) }}`

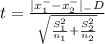
mean((x₁⁻) = 67.798 mean( x₂⁻) = 71.78

variance(S₁²) = 0.663084 variance(S₂²)= 0.727143

S.D(S₁) = 0.814299972 S.D(S₂) = 0.8527267191

standard error (S. e) =
`\sqrt{(S_(1) ^(2) )/(n_(1) ) +(S_(2) ^(2) )/(n_(2) ) }` = 0.396

Now the test statistic

t = 8.79

The degrees of freedom of t- distribution is

ν= n₁+ n₂-2 = 10 +8-2=16

tabulated value = 1.746 for 16 degrees of freedom at 95% level of significance.

Conclusion:-

The null hypothesis is rejected.

we do not compare means between the two data sets

C) 95% of confidence interval for the difference between means

Solution:-

|(x₁⁻ - x₂⁻)| ± tₐ S. e ( (x₁⁻ - x₂⁻)

where standard error (S. e) =
`\sqrt{(S_(1) ^(2) )/(n_(1) ) +(S_(2) ^(2) )/(n_(2) ) }`

given data

mean((x₁⁻) = 67.798 mean( x₂⁻) = 71.78

variance(S₁²) = 0.663084 variance(S₂²)= 0.727143

S.D(S₁) = 0.814299972 S.D(S₂) = 0.8527267191

Standard error =
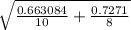`\sqrt{(0.663084 )/(10) +(0.7271 )/(8) }` = 0.396

Standard error = 0.396

The degrees of freedom of t- distribution is

ν= n₁+ n₂-2 = 10 +8-2=16

tabulated value = 1.746 for 16 degrees of freedom at 95% level of significance.

The confidence intervals are

( |(x₁⁻ - x₂⁻)| - tₐ S. e ( (x₁⁻ - x₂⁻), |(x₁⁻ - x₂⁻)| + tₐ S. e ( (x₁⁻ - x₂⁻))

now substitute all values , we get

(|67.798-71.78|-1.746 X (0.396),(|67.798-71.78|+1.746 X (0.396))

on calculation we get

(3.98-0.691 ,3.98+0.691 )

(3.30 ,4.68)

The 95 % of confidence intervals for the difference between means

are (3.30 ,4.68)