Question

On a street map the vertices of a block are w(20,),x(90,30),y(90,120), and z(20,120). The coordinates are measured in yards find the perimeter and area of the block

Answer 1

`\text{Perimeter of wxyz}=320`

`\text{Area of the block}=6300\text{ yards}^2`

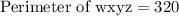
Explanation:

We have been give that one a street map the vertices of a block are w(20,30), x(90,30), y(90,120), and z(20,120). The coordinates are measured in yards. We are asked to find the perimeter and area of the block.

First of all, we will plot our given points on coordinate plane as shown in the attachment.

We can see that block wxyz is in form of a rectangle. We know that perimeter of rectangle is two times the sum of length and width.

The length of the rectangle will be length of segment wx that is the difference between x-coordinates of x and w.

`\text{Length of segment wx}=90-20`

`\text{Length of segment wx}=70`

The width of the rectangle will be length of segment wz that is the difference between y-coordinates of z and w.

`\text{Length of segment wz}=120-30`

`\text{Length of segment wz}=90`

`\text{Perimeter of wxyz}=2(70+90)`

`\text{Perimeter of wxyz}=2(160)`

`\text{Perimeter of wxyz}=320`

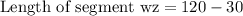
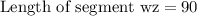
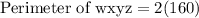
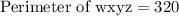
Therefore, the perimeter of the block is 320 yards.

The area of the block will be length times width.

`\text{Area of the block}=\text{70 yards }* \text{90 yards}`

`\text{Area of the block}=6300\text{ yards}^2`

Therefore, the area of the block is 6300 square yards.