Answer:
a) T = 7.5 N
T' = 18.15 N
b) I = 0.016 kgm²
Step-by-step explanation:
Given that:
Mass of the textbook m = 2 kg
Diameter of the pulley d = 0.150 m
Hanged mass m' = 3 kg
Displacement s = 1.2 m
Time t = 0.800 s
According to kinematics equation
Displacement s can be derived from the second equation of motion:
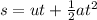
where u = 0
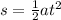
making acceleration a the subject of the formula; we have:

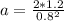
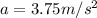
Now; taking into account of mass m;
The tension in the cord attached to the book on the horizontal surfacce can be calculated as:
T = ma
T = 2 × 3.75
T = 7.5 N
For the mass m; the tension is calculated as :
m'g - T' = m' a
T' = m'(g-a)
T' = 3 × (9.8 - 3.75)
T' = 18.15 N
b)
Considering the pulley:
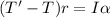
where;
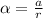
Then

Then the moment of inertia I/ can be re-written as :
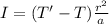
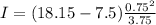
I = 0.016 kgm²