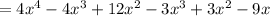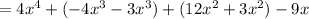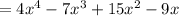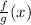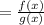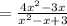Question

Let ​ f(x) = 4(x^2) - 3x

​ g(x) = (x^2) - x + 3.
Find ​(f + g)(x), ​(f - ​g)(x), ​(fg)(x), and (Start Fraction f/g , End Fraction )​(x). Give the domain of each.

Answer 1

(f+g)(x)=5x²-4x+3

(f-g)(x)=3x²-2x+3

(fg)(x)
`=4x^4-7x^3+15x^2-9x`

`(f)/(g)(x)`
`=(4x^2-3x)/(x^2-x+3)`

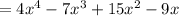
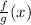
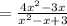
Explanation:

Given that,

f(x)=4x²-3x

g(x)=x²-x+3

(f+g)(x)

=f(x)+g(x)

=4x²-3x+x²-x+3

=(4x²+x²)+(-3x-x)+3 [ combined the like terms]

=5x²-4x+3

(f-g)(x)

=f(x)-g(x)

=4x²-3x-(x²-x+3)

=4x²-3x-x²+x-3

=(4x²-x²)+(-3x+x)-3 [ combined the like terms]

=3x²-2x+3

(fg)(x)

=f(x).g(x)

=(4x²-3x).(x²-x+3)

=4x²(x²-x+3)-3x(x²-x+3)

`=4x^4-4x^3+12x^2-3x^3+3x^2-9x`

`=4x^4+(-4x^3-3x^3)+(12x^2+3x^2)-9x`

`=4x^4-7x^3+15x^2-9x`

`(f)/(g)(x)`

`=(f(x))/(g(x))`

`=(4x^2-3x)/(x^2-x+3)`