Question

The scores of individual students on the American College Testing (ACT) Program composite college entrance examination have a Normal distribution with mean that varies slightly from year to year and standard deviation 6.0. You plan to take an SRS of size n of the students who took the ACT exam this year and compute the mean score of the students in your sample. You will use this to estimate the mean score of all students this year. In order for the standard deviation of to be no more than 0.1, how large should n be?

a. At least 36
b.At least 60
c.At least 600
d.At least 3600
e.This cannot be determined because we do not know the true mean of the population.

Answer 1

Option D) At least 3600

Explanation:

We are given the following in the question:

The distribution of scores of individual students on the American College Testing is a bell shaped distribution that is a normal distribution.

Population standard deviation =

`\sigma = 6.0`

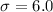
We want that the standard deviation of the sample should not be more than 0.1 that is the standard error should not be more than 0.1

Formula for standard error:

`S.E = (\sigma)/(√(n))`

`S.E\leq 0.1\\\\(\sigma)/(√(n))\leq 0.1\\\\(6)/(√(n))\leq 0.1\\\\√(n)\geq (6)/(0.1)\\\\√(n)\geq 60\\n\geq 3600`

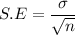
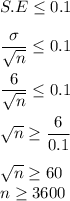
Thus, the sample size must be atleast 3600 so that the sample standard deviation is not more than 0.1.

Thus, the correct answer is

Option D) At least 3600