Question

At the instant shown car A is travelling with a velocity of 24 m/s and which is decreasing at 4 m/s2 along the highway. At the same instant B is travelling on the trumpet interchange curve with a speed of 20 m/s, which is decreasing at 5 m/s2. Determine the relative velocity and relative acceleration of A with respect to B at this instant.

Answer 1

(a) V(A/B) = (14 i - 17.32 J) m/s

(b) acc(A/B) = ( 5.11 i + 5.13 j ) m/s²

Step-by-step explanation:

We will solve with respect to Cartesian vector form.

So,

V(A)= (24i) m/s

acc(A) = (4i) m/s²

There are two components of Car B, cos 60⁰ and sin 60⁰

V(B) = 20 cos 60° i + 20 sin 60° j

V(B) = (10 i + 17.32 j ) m/s

The car B moves along a curve, so it will have a tangential acceleration and a normal acceleration.

The tangential acceleration, a(t) = 5 m/s²

Normal acceleration, a(n) =
`(v^2)/(p) \\\\`

So,

`a(n) = ((20)^2)/(250)\\ \\a(n) = 1.6 m/s^2`

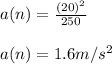
For the tangential acceleration, the acceleration is slowing down. So,

a(t) = (-5 cos 60° i - 5 sin 60° j ) m/s²

a(t) = ( -2.5 i - 4.33 j) m/s²

For normal acceleration, it towards center. So,

a(n) = (1.6 sin 60° i - 1.6 cos 60° j) m/s²

a(n) = (1.39 i - 0.8 j ) m/s²

Total acceleration of Car B:

acc(B) = a(t) + a(n)

acc(B) = ( -2.5 i - 4.33 j) m/s² + (1.39 i - 0.8 j ) m/s²

acc(B) = (-1.11i - 5.13 j ) m/s²

(a) V(A/B) = ?

V(A) = V(B) + V(A/B)

(24i) m/s = (10 i + 17.32 j ) m/s + V(A/B)

V(A/B) = (14 i - 17.32 J) m/s

(b) acc(A/B) = ?

acc(A) = acc(B) + acc(A/B)

(4i) m/s² = (-1.11i - 5.13 j ) m/s² + acc(A/B)

acc(A/B) = ( 5.11 i + 5.13 j ) m/s²