Answer:
the maximum deformation undergone by the spring = 47.46 cm
Step-by-step explanation:
Using conservation of momentum:
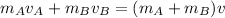
where:
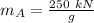
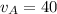
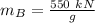

Then;
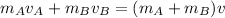

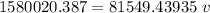

v = 19.375 m/s
However ; using conservation of energy to determine the maximum deformation undergone by the spring ; we have:
![(1)/(2) [m_Av_A^2 +m_Bv_B^2] =(1)/(2)[(m_A+m_B)v^2 + kx^2]](https://img.qammunity.org/2021/formulas/physics/college/akqnxuyrz7pf0d9booo9srgsrefdextjwe.png)
![[m_Av_A^2 +m_Bv_B^2] =[(m_A+m_B)v^2 + kx^2]](https://img.qammunity.org/2021/formulas/physics/college/8tl4m7q2x14psewqlknwe9am76bir1nkud.png)
![[(250*10^3)/(9.81)*40^2 + (550*10^3)/(9.81)*10^2] =[ ((800*10^3)/(9.81) )*19.375^2 + 70 *10^6 \ * x^2]](https://img.qammunity.org/2021/formulas/physics/college/yumnkr8t6nuupz0w6x7f0db7hbqnzpgcqr.png)
x = 0.4746 m
x = 47.46 cm
Thus, the maximum deformation undergone by the spring = 47.46 cm