Question

A 250-kN railroad car A is traveling at 40 m/s while a 550-kN freight car B is traveling at 10 m/s (both cars heading to the right). If the spring constant mounted on car A is k = 70 MN/m, determine the maximum deformation undergone by the spring. Neglect friction.

Answer 1

The maximum deformation undergone by the spring is 0.475 m

Step-by-step explanation:

The conservation of momentum is equal:

`m_(A) v_(A) +m_(B) v_(B) =v(m_(A) +m_(B) )`

Replacing:

`(250x10^(3)*40 )/(9.8) +(550x10^(3)*10 )/(9.8) =v(((250+550)x10^(3) )/(9.8)) \\v=19.375m/s`

The conservation of energy is:

`(1)/(2) (m_(A)v_(A)^(2)+m_(B)v_(B)^(2) )=(1)/(2) (v^(2)(m_(A) +m_(B) )+kx^(2) )\\(250x10^(3)*40^(2) )/(9.8) +(550x10^(3)*10^(2) )/(9.8) =19.375^(2) ((800x10^(3) )/(9.8) )+70x10^(6) x^(2) \\ x=0.475m`

Answer 2

the maximum deformation undergone by the spring = 47.46 cm

Step-by-step explanation:

Using conservation of momentum:

`m_Av_A + m_Bv_B = (m_A+m_B )v`

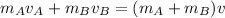
where:

`m_A = (250\ kN)/(g)`

`v_A = 40`

`m_B = (550\ kN)/(g)`

`v_B =10`

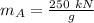
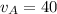
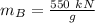
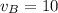
Then;

`m_Av_A + m_Bv_B = (m_A+m_B )v`

`(250*10^3)/(9.81)*40 + (550*10^3)/(9.81)*10 = ((800*10^3)/(9.81) )v`

`1580020.387 = 81549.43935 \ v`

`v = (1580020.387)/(81549.43935)`

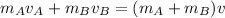
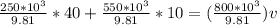
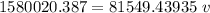
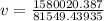
v = 19.375 m/s

However ; using conservation of energy to determine the maximum deformation undergone by the spring ; we have:

`(1)/(2) [m_Av_A^2 +m_Bv_B^2] =(1)/(2)[(m_A+m_B)v^2 + kx^2]`

`[m_Av_A^2 +m_Bv_B^2] =[(m_A+m_B)v^2 + kx^2]`

`[(250*10^3)/(9.81)*40^2 + (550*10^3)/(9.81)*10^2] =[ ((800*10^3)/(9.81) )*19.375^2 + 70 *10^6 \ * x^2]`

x = 0.4746 m

x = 47.46 cm

Thus, the maximum deformation undergone by the spring = 47.46 cm