The length of the diagonal of the rectangle is 6.4 units long.
Explanation:
Step 1:
From the question, we have the length of two sides of the rectangle is 5 units. The points (4, 0) and (4, 4) have the same x coordinates but different y coordinates.
The difference between the y values gives us the length of the other two sides.
So the length of two sides of the rectangle is 5 while the width of the rectangle is 4 units.
Step 2:
With two sides and the diagonal, a right-angled triangle can be formed.
The hypotenuse is the diagonal and assume it is x units long.
The other two sides are 4 and 5 units long.
According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
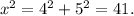
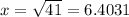 units.
units.
The length of the diagonal of the rectangle is 6.4 units long.