Question

two of the sides of a rectangle have a length of 5 units. The points (4, 0) and (4, 4) are adjacent vertices of a rectangle. To the nearest tenth, what is the length of a diagonal of the rectangle?

Answer 1

The length of the diagonal of the rectangle is 6.4 units long.

Explanation:

Step 1:

From the question, we have the length of two sides of the rectangle is 5 units. The points (4, 0) and (4, 4) have the same x coordinates but different y coordinates.

The difference between the y values gives us the length of the other two sides.

So the length of two sides of the rectangle is 5 while the width of the rectangle is 4 units.

Step 2:

With two sides and the diagonal, a right-angled triangle can be formed.

The hypotenuse is the diagonal and assume it is x units long.

The other two sides are 4 and 5 units long.

According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

`x^(2) = 4^(2) + 5^(2) = 41.`

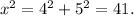
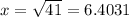`x = √(41) = 6.4031` units.

The length of the diagonal of the rectangle is 6.4 units long.