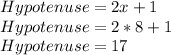Answer:
Hypotenuse = 17cm
Explanation:
From the question we have that,
- It is a right-angled triangle
- The shorter side's length is x
- The hypotenuse's length is 2x + 1
- The other side's length is 2x - 1
Since this is a right-angled triangle, we can apply the Pythagoras formula:
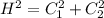
This says that the square of the hypotenuse is the sum of the square of the other sides.
From this, we can replace the variables with the actual values:

We can then expand the exponents to have:
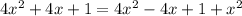
We can proceed to isolate x:
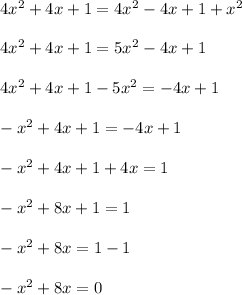
We can now multiply the whole equation by -1 just to have a positive
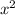 :
:
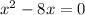
And we can now solve it using Bhaskara:
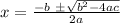
Replacing out values, we've got:

Since x can't be 0 because we're talking about a drawn triangle, x can only be 8.
We can then calculate the hypotenuse based on this value: