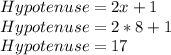Question

2x +1

d A right-angled triangle is drawn so
that the hypotenuse is twice the
shortest side plus 1 cm, and the other
side is twice the shortest side less 1 cm.
Find the length of the hypotenuse.
2x-1

Answer 1

Hypotenuse = 17cm

Explanation:

From the question we have that,

• It is a right-angled triangle
• The shorter side's length is x
• The hypotenuse's length is 2x + 1
• The other side's length is 2x - 1

Since this is a right-angled triangle, we can apply the Pythagoras formula:

`H^(2) = C_(1)^(2) + C_(2)^(2)`

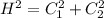
This says that the square of the hypotenuse is the sum of the square of the other sides.

From this, we can replace the variables with the actual values:

`(2x + 1)^(2) = (2x - 1)^(2) + x^(2)`

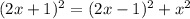
We can then expand the exponents to have:

`4x^(2) + 4x + 1 = 4x^(2) - 4x + 1 + x^(2)`

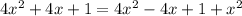
We can proceed to isolate x:

`4x^(2) + 4x + 1 = 4x^(2) - 4x + 1 + x^(2)\\\\4x^(2) + 4x + 1 = 5x^(2) - 4x + 1\\\\4x^(2) + 4x + 1 - 5x^(2) = - 4x + 1\\\\- x^(2) + 4x + 1 = - 4x + 1\\\\- x^(2) + 4x + 1 + 4x = 1\\\\- x^(2) + 8x + 1 = 1\\\\- x^(2) + 8x = 1 - 1\\\\- x^(2) + 8x = 0\\\\`

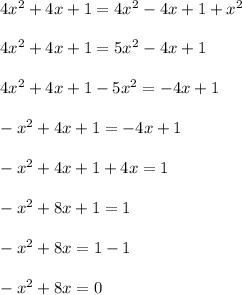
We can now multiply the whole equation by -1 just to have a positive
`x^(2)`:

`x^(2) - 8x = 0`

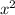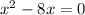
And we can now solve it using Bhaskara:

`x = \frac{-b\ \pm \sqrt{b^(2) - 4ac }}{2a}`

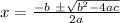
Replacing out values, we've got:

`a = 1\\b = -8\\c = 0\\x = \frac{8\ \pm \sqrt{(-8)^(2) - 4*1*0 }}{2*1}\\x = \frac{8\ \pm \sqrt{(-8)^(2) - 0 }}{2}\\x = (8\ \pm \ 8)/(2)\\x = 0\ or\ x = 8`

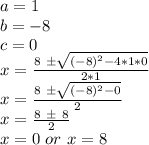
Since x can't be 0 because we're talking about a drawn triangle, x can only be 8.

We can then calculate the hypotenuse based on this value:

`Hypotenuse = 2x + 1\\Hypotenuse = 2*8 + 1\\Hypotenuse = 17`

Answer 2

x = 8

If the hypotenuse = 2x + 1 and the shortest side = x and the other side = 2x - 1

Then we can substitute rose values into the Pythagorus Theorem (a squared plus b squared equals c squared which is the hypotenuse) to the equation in the diagram attached.

Then you just expand the brackets and simplify to get x. Hope that helps.