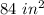Each triangle in the net has a base length that measures 6 inches and a height that measures 4 inches. What is the surface area of the pyramid that can be formed from this net?<…

Question

asked Jan 18, 2021 214k views

2 Answers

Kukudas · Answer 1 · 2021-01-22T16:31:58+0000

Answer:

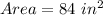
$Area= 84 \ in^2$

Explanation:

The surface area of a pyramid is equivalent to the area of its base plus area of it's 4 triangles.

#The pyramid has a square base with lengths equal to the triangle's base length:

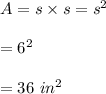
$A=s* s=s^2\\\\=6^2\\\\=36\ in^2$

#The area of the side triangles is calculated as:

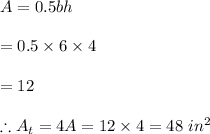
$A=0.5bh\\\\=0.5* 6* 4\\\\=12\\\\\therefore A_t=4A=12* 4=48\ in^2$

We sum the two area to find the net surface area of the pyramid:

$A=A_b+A_t\\\\=36+48\\\\=84\ in^2$

Hence, the pyramid's surface area is
$84 \ in^2$