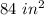Question

Each triangle in the net has a base length that measures 6 inches and a height that measures 4 inches. What is the surface area of the pyramid that can be formed from this net?

Answer 1

its 48

Explanation:

Answer 2

`Area= 84 \ in^2`

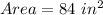
Explanation:

The surface area of a pyramid is equivalent to the area of its base plus area of it's 4 triangles.

#The pyramid has a square base with lengths equal to the triangle's base length:

`A=s* s=s^2\\\\=6^2\\\\=36\ in^2`

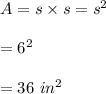
#The area of the side triangles is calculated as:

`A=0.5bh\\\\=0.5* 6* 4\\\\=12\\\\\therefore A_t=4A=12* 4=48\ in^2`

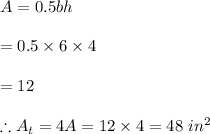
We sum the two area to find the net surface area of the pyramid:

`A=A_b+A_t\\\\=36+48\\\\=84\ in^2`

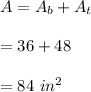
Hence, the pyramid's surface area is
`84 \ in^2`