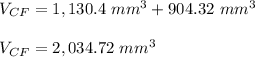Question

The figure is made up of a cylinder and a sphere which has been cut in half. The radius of each half sphere is 6 mm. What is the volume of the composite figure? Use 3.14 for .Round to the nearest hundredth.

Answer 1

Answer:
`2,034.72\ mm^3`

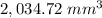
Explanation:

The missing part is: "A cylinder and 2 half spheres. All have a radius of 6 millimeters. The cylinder has a height of 10 millimeters."

You need to use the following formulas to solve the exercise:

1. The volume of a cylinder can be calculated with:

`V_(c)=\pi r^2h`

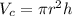
Where "r" is the radius and "h" is the height.

2. The volume of a sphere can be calculated with:

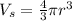`V_(s)=(4)/(3)\pi r^3` Where "r" is the radius.

In this case you know that the cylinder and the sphere have a radius of 6 millimeters and the height of cylinder is 10 millimeters. Then, you can substitute values into each formula in order to find the volumes:

`Vc=(3.14)(6\ mm)^2(10\ mm)\\\\Vc=1,130.4\ mm^3\\\\\\Vs=(4)/(3)(3.14)(6\ mm)^3\\\\Vs=904.32\ mm^3`

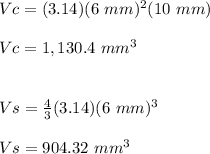
Adding them, you get that the volume of the composite figure is:

`V_(CF)=1,130.4\ mm^3+904.32\ mm^3\\\\V_(CF)=2,034.72\ mm^3`