Question

Please Help:

According to Newton's Law of Cooling, if a body with temperature
`T_(1)` is placed in surroundings with temperature
`T_(0)`, different from that of
`T_(1)`, the body will either cool or warm to temperature
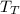
`T_(T)` after t minutes, where:

`T(t)=T_(0) +(T_(1)-T_(0))e^k^t`
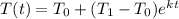
and
`K` is a constant.

If a cup of coffee with temperature 140°F is placed in a freezer with temperature 0°F. The constant k ≅ -0.0815. Use Newton's Law of Cooling to find the coffee's temperature, to the nearest degree Fahrenheit, after 15 minutes.

Answer 1

41°F

Explanation:

T(t) = 0 + (140 - 0)e^(-0.0815t)

T(15) = 140e^(-0.0815×15)

T(15) = 41.22902187

Answer 2

41 degrees F

Explanation:

(Ah, calculus...)

In this case,
`T_0` is 0 degrees F and
`T_1` is 140 degrees F. k = -0.0815 and t = 15. Plug all these values into the equation:

`T(15)=0+(140-0)e^(-0.0815*15) =41.229`

41.229 ≈ 41

So, the answer is 41 degrees F.

Hope this helps!