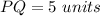Answer:
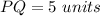
Explanation:
we know that
The Intersecting Secant-Tangent Theorem, states that : If a tangent segment and a secant segment are drawn to a circle from an exterior point, then the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
so
In this problem
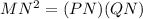
we have
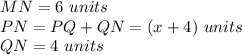
substitute the given values
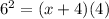
solve for x
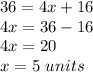
therefore