Question

The length of a rectangle is 7 more than the width. The area is 198 square centimeters. Find the length and width of the rectangle.

Answer 1

he length of a rectangle is 7 more than the width.The area is 800 square centimeters. Find the length and width of the rectangle

Explanation:

Answer 2

Given:

Let l denote the length of the rectangle.

Let w denote the width of the rectangle.

The length of a rectangle is 7 more than the width. This can be written in expression as,

`l=7+w`

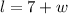
The area of the rectangle is 198 square centimeters.

We need to determine the length and width of the rectangle.

Length and width of the rectangle:

The length and width of the rectangle can be determined using the formula,

`A=length * width`

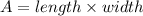
Substituting the values, we have;

`198=(7+w)w`

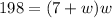
Multiplying, we get;

`198=7w+w^2`

`0=7w+w^2-198`

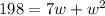
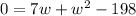
Switch sides, we have;

`w^2+7w-198=0`

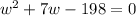
Solving using the quadratic formula, we get;

`w=(-7 \pm √((-7)^2-4(1)(-198)))/(2(1))`

`w=(-7 \pm √(49+792))/(2)`

`w=(-7 \pm √(841))/(2)`

`w=(-7 \pm 29)/(2)`

`w=(-7 +29)/(2) \ or \ w=(-7 -29)/(2)`

`w=(22)/(2) \ or \ w=(-36)/(2)`

`w=11 \ or \ w=-18`

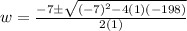
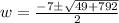
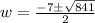
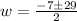
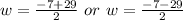
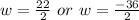
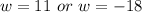
Since, the value of w cannot be negative, thus, w = 11

Thus, the width of the rectangle is 11 cm.

Substituting w = 11 in the equation
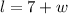`l=7+w`, we get;

`l=7+11`

`l=18`

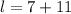
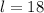
Thus, the length of the rectangle is 18 cm.

Hence, the length and width of the rectangle are 18 cm and 11 cm respectively.