Given:
Let l denote the length of the rectangle.
Let w denote the width of the rectangle.
The length of a rectangle is 7 more than the width. This can be written in expression as,
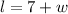
The area of the rectangle is 198 square centimeters.
We need to determine the length and width of the rectangle.
Length and width of the rectangle:
The length and width of the rectangle can be determined using the formula,
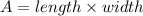
Substituting the values, we have;
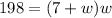
Multiplying, we get;
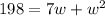
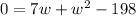
Switch sides, we have;
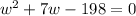
Solving using the quadratic formula, we get;
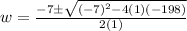
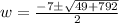


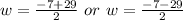
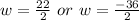
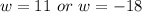
Since, the value of w cannot be negative, thus, w = 11
Thus, the width of the rectangle is 11 cm.
Substituting w = 11 in the equation
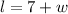 , we get;
, we get;

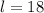
Thus, the length of the rectangle is 18 cm.
Hence, the length and width of the rectangle are 18 cm and 11 cm respectively.