Question

A binomial probability experiment is conducted with the given parameters. Use technology to find the probability of x successes in the n independent trials of the experiment.n=9,p=0.25,x<4

Answer 1

Therefore the required probability is 0.83427.

Explanation:

Binomial (n,p) distribution:

A discrete random variable X having the set {0,1,2,3.....,n} as the spectrum, is said to have binomial distribution with parameter n=the number of trial in the binomial experiment,p= the probability of success on an individual trial, if the probability mass function of X is given by

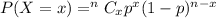`P(X=x)=^nC_x p^x(1-p)^(n-x)` for x= 0,1,2,....

=0 elsewhere

where n is a positive integer and 0<p<1.

`^nC_x=(n!)/(r!(n-r)!)`

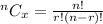
Given that,

n= 9 and p=0.25

We are interested to find P(x<4).

P(x<4)

=P(x=0)+P(x=1)P(x=2)+P(x=3)

`=^9C_0 (0.25)^0(1-0.25)^(9-0)+^9C_1 (0.25)^1(1-0.25)^(9-1)+^9C_2 (0.25)^2(1-0.25)^(9-2)+^9C_3 (0.25)^3(1-0.25)^(9-3)`

`=\{1* 1* (0.75)^9\}+\{9* 0.25* (0.75)^8\}+\{36 * (0.25)^2* (0.75)^7\}+\{84* (0.25)^3* (0.75)^6\}`

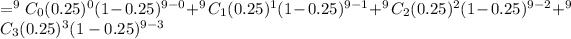
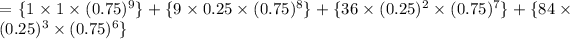
≈ 0.83427

Therefore the required probability is 0.83427.