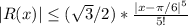Answer:
Explanation:
By the general expresion:
T4(x) = f(a) + (f'(a)/1!)*(x-a) + (f''(a)/2!)*(x-a)² + (f'''(a)/3!)*(x-a)³ + (f''''(a)/4!)*(x-a)^4
Then:
f(x) = sinx ; f'(x) = cosx ; f''(x) = -sinx ; f'''(x) = -cosx ; f''''(x) = sinx
Since: sin(π/6) = 1/2 ; cos(π/6) =
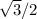
Thus, in the expresion for T4(x):
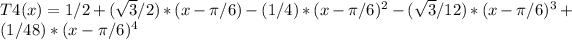
Inequality, by the Taylor's theorem (jpg adjunt):
We need to find M in the interval indicate. Of the analysis from the graf of the function (jpg adjunt), we see a good candidate is:
M = f(π/3) = sin(π/3) =
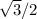
Then, in the Taylor's theorem: