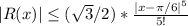Question

10. (a) Find T4(x), the 4th degree Taylor polynomial for f(x) = sin x centered at a = π/6. (b) Use Taylor’s inequality to estimate the accuracy of the approximation f(x) ≈ T4(x) when 0 ≤ x ≤ π/3. In

Answer 1

(a)
`T_4((\pi)/(6))=(1)/(2)+(√(3))/(2)(x-(\pi)/(6))-(1)/(2*2!)(x-(\pi)/(6))^2-(√(3))/(2*3!)(x-(\pi)/(6))^3+(1)/(2*4!)(x-(1)/(2))^4`

(b)
`R_4(x)=(f^((5))(\alpha))/((5!))(x-(\pi)/(6))^5=(cos\alpha)/(5!)(x-(\pi)/(6))^5`

Explanation:

(a) We have that Taylor's polynomial is given by

`T_n(x)=f(a)+f'(a)(x-a)+(f''(a))/(2!)(x-a)^2+...+(f^((n))(a))/(n!)(x-a)^n`

In this case we have to compute T4, with a = pi\6. Hence we have to calculate the first derivative until the fourth derivative of f(x):

`f(x)=sinx \ ; \ f((\pi)/(6))=sin((\pi)/(6))=0.5\\\\f'(x)=cosx \ ; \ f'((\pi)/(6))=cos((\pi)/(6))=(√(3))/(2)\\\\f''(x)=-sinx \ ; \ f''((\pi)/(6))=-sin((\pi)/(6))=-0.5\\\\f'''(x)=-cosx \ ; \ f'''((\pi)/(6))=-cos((\pi)/(6))=-(√(3))/(2)\\\\f^((4))=sinx \ ; \ f^((4))((\pi)/(6))=sin((\pi)/(6))=0.5`

By replacing we have

`T_4((\pi)/(6))=(1)/(2)+(√(3))/(2)(x-(\pi)/(6))-(1)/(2*2!)(x-(\pi)/(6))^2-(√(3))/(2*3!)(x-(\pi)/(6))^3+(1)/(2*4!)(x-(1)/(2))^4`

(b) the Taylor's inequality is given by

`|R_n(x)|\leq (M)/((n+1)!)|x-a|^(n+1)\\\\R_(x)=(f^((n+1))(\alpha))/((n+1)!)(x-a)^n+1`

where f(x)<=M, Hence we have

`R_4(x)=(f^((5))(\alpha))/((5!))(x-(\pi)/(6))^5=(cos\alpha)/(5!)(x-(\pi)/(6))^5`

HOPE THIS HELPS!

Answer 2

Explanation:

By the general expresion:

T4(x) = f(a) + (f'(a)/1!)*(x-a) + (f''(a)/2!)*(x-a)² + (f'''(a)/3!)*(x-a)³ + (f''''(a)/4!)*(x-a)^4

Then:

f(x) = sinx ; f'(x) = cosx ; f''(x) = -sinx ; f'''(x) = -cosx ; f''''(x) = sinx

Since: sin(π/6) = 1/2 ; cos(π/6) =
`√(3)/2`

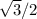
Thus, in the expresion for T4(x):

`T4(x) = 1/2 + (√(3)/2 )*(x-\pi/6) - (1/4)*(x-\pi/6)^(2) - (√(3)/12)*(x-\pi/6)^(3) + (1/48)*(x-\pi/6)^(4)`

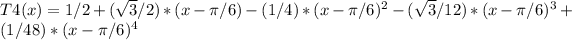
Inequality, by the Taylor's theorem (jpg adjunt):

We need to find M in the interval indicate. Of the analysis from the graf of the function (jpg adjunt), we see a good candidate is:

M = f(π/3) = sin(π/3) =
`√(3)/2`

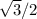
Then, in the Taylor's theorem:

`|R(x)| \leq (√(3)/2)* (|x-\pi/6 |^(5) )/(5!)`