Question

3200 is placed in an account with an annual interest rate of 5.25% to the nearest tenth of a year how long will it take for the account value to reach 13400

Answer 1

Answer: 28.0 years

Explanation:

The formula we use to find the compounded amount after t years by putting a rate r on Principal value P is :

`A=P(1+r)^x`

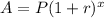
As per given , we have

P=$3200 , r=5.25%=0.0525 , A= $13400

Put all values in formula , we get

`13400=3200(1+0.0525)^x\\\\\Rightarrow\ (1.0525)^x=(13400)/(3200)=4.1875\\\\\Rightarrow\ (1.0525)^x=4.1875`

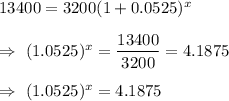
Taking log on both sides , we get

`x\log(1.0525)=\log(4.1875)\\\\\Rightarrow x(0.0222221045077)=0.621954820045\\\\\Rightarrow\ x=(0.621954820045)/(0.0222221045077)=27.9881151594\approx28.0`

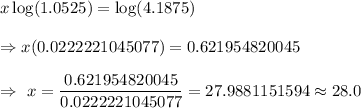
Hence, it will take 28.0 years .