Question

Postal regulations specify that a parcel sent by priority mail may have a combined length and girth of no more than 126 in. Find the dimensions of a rectangular package that has a square cross section and largest volume that may be sent by priority mail.

Answer 1

The package of maximum dimensions has:

Width and height = 21 in each , and length = 42 in

Explanation:

A package of square cross section has a girth equal to the perimeter of the square ("4 x" if we consider "x" as the side of the square). This quantity, added to the package's length "L" has to be no more than 126 in.

The maximum allowed for priority mail is therefore:
`4x+L=126 \,in`

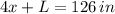
At the same time, we want the volume of the package to be a maximum. The volume of this parcel is defined as the product of all three dimensions of the package:

`V=width\,*\,height\,*\,length\\V=x\,*\,x\,*\,L\\V=x^2\,L`

We can now use the first formula for the priority mail maximum dimensions, to write L in terms of "x" and replace it in the volume formula:

`4x+L=126 \,in\\L=126-4x`

So now the volume expression becomes:

`V=x^2\,(126-4x)=126x^2-4\,x^3`

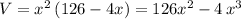
If the student doesn't know calculus, a graphing tool can be used to find the maximum.

With calculus derivatives the maximum can be easily found:

We can request the derivative of the volume to satisfy the conditions for derivative = 0 and the function concave down to locate the function's "maximum".

`V'(x)=252\,x-12\,x^2\\0=252\,x-12\,x^2\\0=12\,x\,(21-x)`

This tells us that there are two solutions to the derivative equal zero:

`x=0\,\,and\,\,x=21`

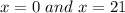
The first solution is clearly a minimum since it would render a package of zero volume. the second solution (
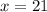`x=21`) is the one that corresponds to the maximum of the volume function.

Therefore, the dimensions of the package of largest volume are: width and height: 21 in each, and length L= 126 - 4*21 = 42 in