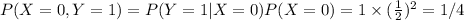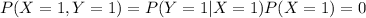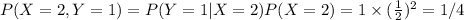Answer:
Explanation:
It can be clearly observed that
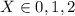 and
and
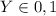
Now lets find the probabilities of all possible combinations

Since it is impossible that the coin ha flipped in different ways given that all the time the tail has fallen
 =1/2
=1/2
 =1/2
=1/2
and similarly,