Question

A particle carrying charge +q is placed at the center of a thick-walled conducting shell that has inner radius R and outer radius 2R and carries charge −2q. A thin-walled conducting shell of radius 5R carries charge +2q and is concentric with the thick-walled shell. Define V = 0 at infinity. Calculate all distances from the particle at which the electrostatic potential is zero.

Answer 1

10R/11 and 5R/2

Step-by-step explanation:

The radius of the conducting shell = R,

Electrostatic potential inside the shell (r<R) = kq/R

Electrostatic potential outside the shell (r>R) = kq/r

If x is the point of zero potential

Electrostatic potential for inner shell,
`V_(1) = (kq)/(X - R)`

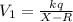
Electrostatic potential for outer shell,
`V_(2) = (-2kq)/(X - 2R)`

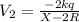
Electrostatic potential for the thin walled shell,
`V_(3) = (2kq)/(X - 5R)`

`V_(1) + V_(2) + V_(3) = 0`

`(kq)/(X-R) - (2kq)/(X-2R) + (2kq)/(X-5R) = 0`

`(1)/(X-R) - (2)/(X-2R) + (2)/(X-5R) = 0\\(X-R) - 2(X-R)(X-5R)+2(X-R)(X-2R) = 0`

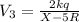
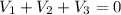
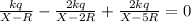
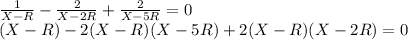
The values of X=r that satisfy the above equation are 10R/11 and 5R/2