Answer:
10R/11 and 5R/2
Step-by-step explanation:
The radius of the conducting shell = R,
Electrostatic potential inside the shell (r<R) = kq/R
Electrostatic potential outside the shell (r>R) = kq/r
If x is the point of zero potential
Electrostatic potential for inner shell,

Electrostatic potential for outer shell,
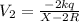
Electrostatic potential for the thin walled shell,

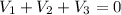
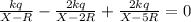

The values of X=r that satisfy the above equation are 10R/11 and 5R/2