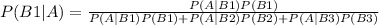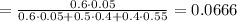Question

Suppose the events Upper B 1​, Upper B 2​, and Upper B 3​, are mutually exclusive and complementary​ events, such that ​P(Upper B 1​)equals0.05​,​ P(Upper B 2​)equals0.4​, and ​P(Upper B 3​)equals0.55. Consider another event A such that ​P(A|Upper B 1​)equals0.6​, ​P(A|Upper B 2​)equals0.5​, and ​P(A|Upper B 3​)equals0.4. Use​ Bayes's Rule to find ​P(Upper B 1​|A).

Answer 1

0.0666

Explanation:

We have three events that we are said are mutually exclusive and complementary. That is, the union of the three events is the sample space. This is confirmed by checking that the probabilities of B1, B2 and B3 add up to 1. P(B1) = 0.05, P(B2)=0.4 and P(B3) = 0.55 do add up to 1.

Consider the definition of conditional probability. Given two events A,B such that P(B)>0 we have that

`P(A|B) = (P(A\cap B))/(P(B))`

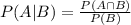
Note that this implies that

`P(A\cap B) = P(A|B) \cdot P(B)`

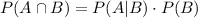
We have that,

`P(B1|A) = (P(B1\cap A))/(P(A))= (P(A|B1)P(B1))/(P(A))`

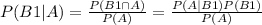
Note that from that expression, we are only missing P(A). REcall that since B1,B2 and B3 union up to the sample space, we have that

`A = (A\cap B1) \cup (A\cap B2) \cup (A \cap B3)`

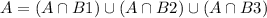
Hence, since this three sets are disjoint, we have that

`P(A) = P(A\cap B1) + P(A\cap B2)+ P(A \cap B3)`

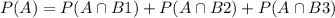
Using the previous relation that we had, we have that

`P(A) = P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)P(B3)`

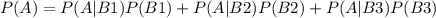
Then, the final answer is

`P(B1|A) = (P(A|B1)P(B1))/(P(A|B1)P(B1)+P(A|B2)P(B2)+P(A|B3)P(B3))`

`=(0.6 \cdot 0.05)/(0.6 \cdot 0.05 + 0.5\cdot 0.4+ 0.4\cdot 0.55) =0.0666`