Question

A rectangular garden of area 480 square feet is to be surrounded on three sides by a brick wall costing $ 12 per foot and on one side by a fence costing $ 8 per foot. Find the dimensions of the garden such that the cost of the materials is minimized

Answer 1

Therefore the dimensions of the rectangular garden are 23.42 ft by 20.5 ft.

Explanation:

Given that,

A rectangular garden of area 480 square feet.

Let length of the rectangular garden be x which is surrounded by fence and width of the rectangular garden be y.

Then xy is the area of the given rectangular garden .

Then,

xy= 480

`\Rightarrow y=(480)/(x)`

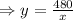
The length of the tree sides which are surrounded by brick wall is = 2y+x.

The cost for the brick wall is =Length×cost per feet= $12(2y+x)

The cost for the fencing is =Length×cost per feet= $ 9x

`\therefore C=12(2y+x)+9x`

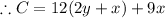
Now putting
`y=(480)/(x)`

`\therefore C=12(2.(480)/(x)+x)+9x`

`\Rightarrow C=(11520)/(x)+21x`

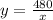
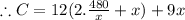
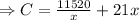
Differentiating with respect to x

`C'=-(11520)/(x^2)+21`

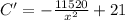
Again differentiating with respect to x

`C''=(23040)/(x^3)`

Now we set C'=0

`\therefore-(11520)/(x^2)+21=0`

`\Rightarrow(11520)/(x^2)=21`

`\Rightarrow x^2=(11520)/(21)`

`\Rightarrow x\approx 23.42`

`C''|_(x=23.42)=(23040)/((23.42)^3)>0`.

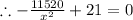
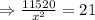
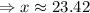
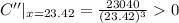Since at x=23.42,C''>0. So at x=23.42, the total cost will be minimum.

The width of the rectangular garden is
`y=(480)/(x)`

`=(480)/(23.42)`

`\approx 20.5`

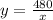
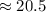
Therefore the dimensions of the rectangular garden are 23.42 ft by 20.5 ft.

The cost of the material is
`C=(11520)/(x)+21x`

`=(11520)/(23.42)+21* 23.42`

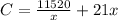
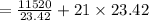
=$983.70