Answer:
Therefore the dimensions of the rectangular garden are 23.42 ft by 20.5 ft.
Explanation:
Given that,
A rectangular garden of area 480 square feet.
Let length of the rectangular garden be x which is surrounded by fence and width of the rectangular garden be y.
Then xy is the area of the given rectangular garden .
Then,
xy= 480
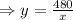
The length of the tree sides which are surrounded by brick wall is = 2y+x.
The cost for the brick wall is =Length×cost per feet= $12(2y+x)
The cost for the fencing is =Length×cost per feet= $ 9x
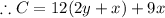
Now putting
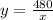
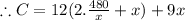
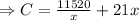
Differentiating with respect to x
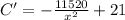
Again differentiating with respect to x
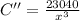
Now we set C'=0
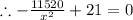
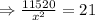
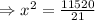
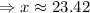
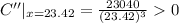 .
.
Since at x=23.42,C''>0. So at x=23.42, the total cost will be minimum.
The width of the rectangular garden is
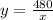
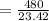
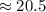
Therefore the dimensions of the rectangular garden are 23.42 ft by 20.5 ft.
The cost of the material is
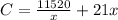
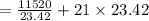
=$983.70