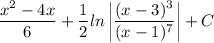Question

`\int\ (x^3-6x^2+9x+3)(3x^2-12x+9) dx`

Answer 1

If the integral is simply

`\displaystyle\int(x^3-6x^2+9x+3)(3x^2-12x+9)\,\mathrm dx`

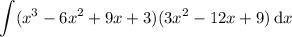
then notice that

`\mathrm d(x^3-6x^2+9x+3)=(3x^2-12x+9)\,\mathrm dx`

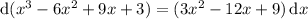
which means you can compute the integral easily with a substitution

`u=x^3-6x^2+9x+3\implies\mathrm du=(3x^2-12x+9)\,\mathrm dx`

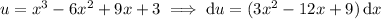
Under this transformation, the integral is

`\displaystyle\int u\,\mathrm du=\frac{u^2}2+C=\boxed{\frac{(x^3-6x^2+9x+3)^2}2+C}`

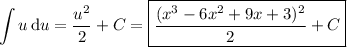
On the other hand, in case you're missing a symbol and the integral is actually

`\displaystyle\int(x^3-6x^2+9x+3)/(3x^2-12x+9)\,\mathrm dx`

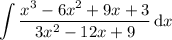
then first carry out the division:

`(x^3-6x^2+9x+3)/(3x^2-12x+9)=\frac x3-\frac23-(2x-9)/(3x^2-12x+9)`

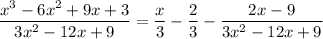
Now,
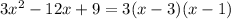`3x^2-12x+9=3(x-3)(x-1)`, so to integrate the remainder term you can decompose it into partial fractions:

`-(2x-9)/(3(x-3)(x-1))=\frac a{x-3}+\frac b{x-1}`

`9-2x=a(x-1)+b(x-3)`

`x=1\implies7=-2b\implies b=-\frac72`

`x=3\implies3=2a\implies a=\frac32`

`\implies-(2x-9)/(3(x-3)(x-1))=\frac 3{2(x-3)}-\frac 7{2(x-1)}`

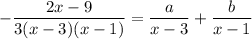
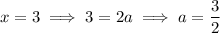
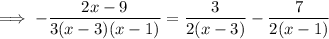
Then the integral would be

`\displaystyle\int(x^3-6x^2+9x+3)/(3x^2-12x+9)\,\mathrm dx=\boxed{\frac{x^2}6-\frac{2x}3+\frac32\ln|x-3|-\frac72\ln|x-1|+C}`

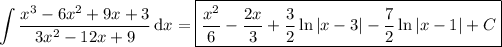
which can be rewritten in several ways, such as

`\frac{x^2-4x}6+\frac12ln\left|((x-3)^3)/((x-1)^7)\right|+C`