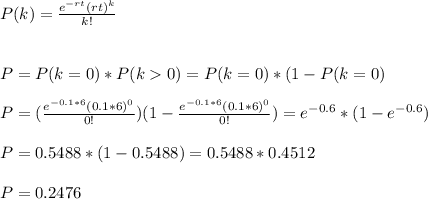Question

Automobile warranty claims for engine mount failure in a Troppo Malo 2000 SE are rare at a certain dealership, occurring at a mean rate of 0.1 claim per month. (a) What is the probability that the dealership will wait at least 6 months until the next claim? (Round your answer to 4 decimal places.) Probability (b) What is the probability that the dealership will wait at least a year? (Round your answer to 4 decimal places.) Probability (c) What is the probability that the dealership will wait at least 2 years? (Round your answer to 4 decimal places.) Probability (d) What is the probability that the dealership will wait at least 6 months but not more than 1 year? (Round your answer to 4 decimal places.) Probability

Answer 1

a) Probability: 0.5488

b) Probability: 0.3012

c) Probability: 0.0907

d) Probability: 0.2476

Explanation:

a) We can model this as a Poisson process, with parameter r=0.1.

We have to calculate the probability that no claim is made in 6 months.

`P(k)=(e^(-rt)(rt)^k)/(k!) \\\\\\P(k=0)=(e^(-0.1*6)(0.1*6)^0)/(0!)=e^(-0.6)=0.5488`

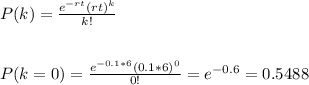
The probability that the dealership will wait at least 6 months until the next claim is 0.5488.

b) In this case, t=12 months.

`P(k)=(e^(-rt)(rt)^k)/(k!) \\\\\\P(k=0)=(e^(-0.1*12)(0.1*12)^0)/(0!)=e^(-1.2)=0.3012`

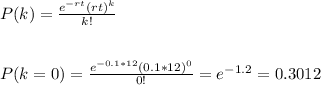
c) In this case, t=24 months

`P(k)=(e^(-rt)(rt)^k)/(k!) \\\\\\P(k=0)=(e^(-0.1*24)(0.1*24)^0)/(0!)=e^(-2.4)=0.0907`

d) In this case, we have to multiply the probability that there is no claim in the first 6 months (k=0, t=6) and the probability that there is more than one claim in the next 6 months (k>0, t=6).

As the Poisson process is memoryless, the probabilitiies are independent of past events and can be calculated that way.

`P(k)=(e^(-rt)(rt)^k)/(k!) \\\\\\P=P(k=0)*P(k>0)=P(k=0)*(1-P(k=0)\\\\P=((e^(-0.1*6)(0.1*6)^0)/(0!))(1-(e^(-0.1*6)(0.1*6)^0)/(0!))=e^(-0.6)*(1-e^(-0.6))\\\\P=0.5488*(1-0.5488)=0.5488*0.4512\\\\P=0.2476`