Question

What is the ratio of the volume of Sphere A to the volume of Sphere B?

sphere A: 4 inch radius. sphere B: 3 inch radius.

Answer 1

Answer : The ratio of the volume of Sphere A to the volume of Sphere B is, 64 : 27

Step-by-step explanation :

Formula used to calculate the volume of sphere is:

`V=(4)/(3)\pi r^3`

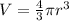
First we have to calculate the volume of sphere A.

Given:

r = radius of sphere A = 4 inch

`V_A=(4)/(3)\pi (4)^3`

`V_A=(256)/(3)\pi \text{ inch}^3`

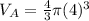
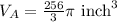
Now we have to calculate the volume of sphere B.

Given:

r = radius of sphere B = 3 inch

`V_B=(4)/(3)\pi (3)^3`

`V_B=36\pi \text{ inch}^3`

Now we have to calculate the ratio of the volume of Sphere A to the volume of Sphere B.

`(V_A)/(V_B)=\frac{(256)/(3)\pi \text{ inch}^3}{36\pi \text{ inch}^3}`

`(V_A)/(V_B)=(64)/(27)`

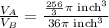
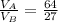
Therefore, the ratio of the volume of Sphere A to the volume of Sphere B is, 64 : 27