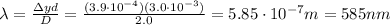Question

A beam of yellow light is made to pass through two slits that are 3.0 x 10−3 meters apart. On a screen 2.0 meters away from the slits, an interference pattern appears with bands of light separated by 3.9 x 10−4 meters. What is the wavelength of the light?

Answer 1

5.9 x 10^-7 m

Step-by-step explanation:

I took the test :)

Answer 2

585 nm

Step-by-step explanation:

The formula that gives the position of the m-th maximum (bright fringe) relative to the central maximum in the interference pattern produced by diffraction from double slit is:

`y=(m\lambda D)/(d)`
`\Delta y =(m\lambda D)/(d)`

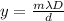
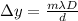
where

m is the order of the maximum

`\lambda` is the wavelength

D is the distance of the screen from the slits

d is the separation between the slits

The distance between two consecutive bright fringes therefore is given by:

`\Delta y = ((m+1)\lambda D)/(d)-(m\lambda D)/(d)=(\lambda D)/(d)`

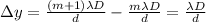
In this problem we have:

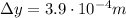`\Delta y = 3.9\cdot 10^(-4) m` (distance between two bright fringes)

D = 2.0 m (distance of the screen)

d = 3.0 x 10−3 m (separation between the slits)

Solving for
`\lambda`, we find the wavelength:

`\lambda=(\Delta y d)/(D)=((3.9\cdot 10^(-4))(3.0\cdot 10^(-3)))/(2.0)=5.85\cdot 10^(-7) m = 585 nm`