Question

Given sin B = .45 find angle B in radians. Round your answer to the nearest hundredth.

Answer 1

We get the value of
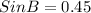`Sin B=0.45` in radians which is equal to
`0.15\pi`

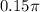
Explanation:

Given that,

`Sin B=0.45`

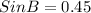
To find:- find angle B in Radians.

So,

To find the Angle B needs to take
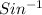`Sin^(-1)`. Sin has a range
`[-1,1]` for all
`\theta`∈
`R`.

`Sin B=0.45`

`B=Sin^(-1) (0.45)`

`B=26.74`

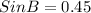
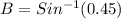
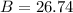
Thus angle
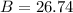`B=26.74` is in degree.

Here, converting the degree into radian we find,

`Radian = degree * (\pi)/(180)`

⇒
`B= 26.74 * (\pi)/(180)\ Rad`

⇒
`B = 0.15\pi\ Rad`

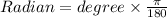
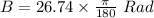
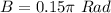
Therefore,

We get the value of
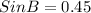`Sin B=0.45` in radians which is equal to
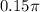`0.15\pi`.