Question

Haylee hikes to the top of a 120-foot vertical cliff. From the top of the cliff, the angle of depression to her campsite is 10∘. How far away from the campsite is the base of the cliff? Round to the nearest foot.

Answer 1

681 feet

Explanation:

Let x represent the distance between campsite and the base of the cliff.

We have been given that Haylee hikes to the top of a 120-foot vertical cliff. From the top of the cliff, the angle of depression to her campsite is 10∘. We are asked to find the distance between campsite and the base of the cliff.

We can see that angle of depression forms a right triangle with respect to ground, cliff and campsite.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

`\text{tan}(10^(\circ))=(120)/(x)`

`x=\frac{120}{\text{tan}(10^(\circ))}`

`x=(120)/(0.176326980708)`

`x=680.5538183559`

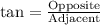
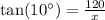
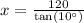
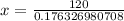
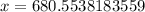
Upon rounding to nearest foot, we will get:

`x\approx 681`

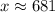
Therefore, the campsite is 681 feet away from the base of the cliff.